Work in Progress

Sono iniziati gli incontri pomeridiani dai quali nasceranno nuovi post .... stiamo lavorando per voi!!! ... WORK IN PROGRESS 

CENTERED (Un filmato in cui è protagonista la simmetria)

Wes Anderson, regista statunitense vincitore del Golden Globe 2015 con il film "The Grand Budapest Hotel", è "ossessionato" dalla simmetria. Godetevi questo breve filmato intitolato "Centered" in cui una linea bianca tratteggiata rende visibile l'asse di simmetria di ciascun fotogramma.

LE ISOMETRIE

Le isometrie sono trasformazioni geometriche grazie alle quali tutti i punti di una figura vengono trasportati nei punti di un'altra figura lasciandone inalterate la lunghezza dei segmenti e l’ampiezza degli angoli, ovvero le figure vengono semplicemente spostate senza essere deformate. 

L’unica cosa che cambia è la loro posizione, mentre, cosa molto importante, conservano perimetro e area.

Le isometrie sono anche dette "movimenti rigidi" del piano

Esse sono:

1. traslazioni
2. simmetrie (assiali e centrali)
3. rotazioni
4. glissosimmetrie (o antitraslazioni)

LA TRASLAZIONE

La traslazione è il movimento rigido di una figura su un piano lungo una direzione e secondo un verso assegnato

La traslazione è caratterizzata da tre elementi:

1.    direzione (la retta passante per i punti corrispondenti)

2.    verso o senso

3.    intensità o modulo  (rappresentata dalla misura della lunghezza dello spostamento)

I tre elementi vengono rappresentati insieme con un segmento orientato detto vettore.

Nella traslazione restano inalterate la FORMA e la DIMENSIONE mentre cambia la POSIZIONE.

Tutti i punti si spostano nella stessa direzione e della stessa distanza.

Anche Geogebra ci viene in aiuto se vogliamo creare figure che traslano sul piano (1)

Possiamo concludere che la traslazione è un movimento rigido lungo una linea retta che non deforma la figura, infatti, ogni lato della figura di partenza ha mantenuto la sua lunghezza, ogni angolo la sua ampiezza.  Quindi...non sono variate  né  la forma: la figura di partenza e quella traslata sono congruenti.

Poiché la figura traslata ha mantenuto anche la sua orientazione, la traslazione si dice isometria diretta.

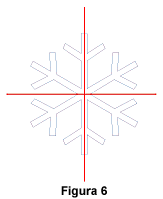
LA SIMMETRIA

Simmetria significa in greco "con misura", "con armonia" e sia in natura, che nell’arte esistono molti esempi di simmetria, che spesso concorre direttamente alla bellezza degli oggetti in cui si manifesta.

Può essere assiale o centrale.

Mosaici della sala di Re Ruggero nel Palazzo dei Normanni a Palermo (890 a.C. circa)

                                                           Cattedrale di Nôtre Dame a Parigi

Vaso greco

Monumento alla fratellanza umana di Bruno Giorgi a Brasilia

Michelangelo da Caravaggio, Narciso, circa 1600.

Simmetria assiale

Data una retta r, la simmetria assiale di asse r è la trasformazione del piano in sé che lascia fissi tutti i punti di r e che ad ogni punto P del piano, esterno ad r, fa corrispondere il punto P’ tale che la retta r sia perpendicolare al segmento PP’ e lo tagli nel suo punto medio.

La retta che taglia una figura in due parti uguali, perfettamente sovrapponibili si chiama asse di simmetria (2).

Molti sono i Poligoni che possiedono uno o più assi di simmetria.

O figure qualunque:

Gioca un po’ con la simmetria assiale! (3)

È possibile ottenere una simmetria assiale semplicemente usando uno specchio.

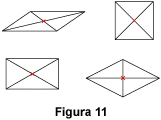
Simmetria centrale

La simmetria centrale di centro C è una trasformazione che ad ogni punto P del piano associa un punto P' tale che C è il punto medio del segmento PP' e si dice centro di simmetria (4).

Il centro di simmetria di un segmento è il suo punto medio.

Tutti i punti di una retta sono suoi centri di simmetria (la retta è infinitamente estesa).

Il centro di simmetria di un cerchio è il centro del cerchio.

Il centro di simmetria di un parallelogramma, in particolare di un quadrato, di un rettangolo o di un rombo, è il punto d’intersezione delle sue diagonali.

Il centro di simmetria di un poligono regolare avente un numero pari di lati è il centro della circonferenza circoscritta al poligono stesso.

Ricapitolando … si definiscono figure con un centro di simmetria le figure che vengono trasformate in sé dalla simmetria centrale attorno a quel punto.

Controlla se hai capito mettendoti alla prova con un semplice esercizio (5).

Possiamo concludere che … la simmetria è una  trasformazione che non deforma la figura, infatti ogni lato della figura di partenza ha mantenuto la sua lunghezza e ogni angolo la sua ampiezza, quindi...non essendo variate né le dimensioni né la forma, la figura di partenza e quella simmetrica sono  congruenti

La simmetria (assiale) è un’isometria inversa poiché inverte l’orientazione della figura.

LA ROTAZIONE

La rotazione è una trasformazione isometrica che fa ruotare ogni punto della figura di uno stesso angolo rispetto a un punto fisso del piano detto centro di rotazione, dunque è caratterizzata da un punto fisso (che chiamiamo O e che la trasformazione lascia invariato) e dall’ampiezza di un angolo (che chiamiamo alfa).

La rotazione può avvenire in senso orario o antiorario (6)

Possiamo concludere che la rotazione non deforma la figura, infatti ogni lato della figura di partenza ha mantenuto la sua lunghezza ogni angolo la sua ampiezza, quindi...non essendo variate né le dimensioni né la forma, la figura di partenza e quella simmetrica sono  congruenti.

La rotazione è una isometria diretta.

LA GLISSOSIMMETRIA

Una glissosimmetria è una composizione di una simmetria assiale con una traslazione; può sempre essere pensata come la composizione di una particolare simmetria assiale con una traslazione nella direzione dell’asse di simmetria.

Si tratta di una isometria indiretta.

Arrivati alla fine di questo lungo percorso ...

 ... giochiamo ancora (7) ... per l'ultima volta!

«AREA E PERIMETRO»

Attività di gruppo su rettangoli isoperimetrici e rettangoli equivalenti

Molti colgono intuitivamente che tra perimetro e area di una poligono o di più poligoni esistono delle relazioni, ma non sempre riescono a capire di che tipo di relazioni si tratti ... , anzi spesso quel che si pensa non corrisponde alla realtà.

Siamo partiti dallo studio di perimetro e area del rettangolo, andando poi a sperimentare che tipo di relazione esista tra le aree di rettangoli isoperimetrici (con lo stesso perimetro) e tra i perimetri di rettangoli equivalenti (con la stessa area).

Siamo partiti da questa domanda:

"Due o più rettangoli che hanno lo stesso perimetro hanno anche la stessa area?"

Dopo un rapido confronto sulle idee di ciascuno, per poter arrivare ad una risposta adeguata e certa alla domanda posta, abbiamo "costruito" rettangoli con lo stesso perimetro usando un cordoncino lungo 20 cm, dopo averne annodato le estremità.

Con dei semplici gesti, modificando la distanza tra le dita, abbiamo ottenuto alcuni dei tanti possibili rettangoli, tutti con perimetro di 20 cm, essendo il cordoncino sempre lo stesso (e non essendo elastico).

Abbiamo poi registrato alcuni dei possibili valori di base e altezza dei rettangoli ottenuti in una prima tabella e poi in una seconda tabella, per ciascun rettangolo considerato, abbiamo riportato la lunghezza della base e l'area corrispondente.

Osservando i dati relativi alle aree dei diversi rettangoli abbiamo finalmente trovato la risposta alla nostra domanda:

"le aree di rettangoli isoperimetrici non sono tutte uguali" 

Inoltre siamo arrivati anche alla conclusione che ... 

il rettangolo di area massima è il quadrato.

Siamo rimasti sorpresi nello scoprire che  il quadrato è anch'esso un rettangolo, ma un rettangolo «speciale» infatti, oltre ad avere tutti gli angoli congruenti (caratteristica di tutti quei parallelogrammi che possiamo chiamare rettangoli), ha anche tutti i lati congruenti, quindi è un poligono regolare.

Con gli stessi dati abbiamo costruito un diagramma cartesiano e unendo i punti abbiamo ottenuto una curva chiamata "parabola".

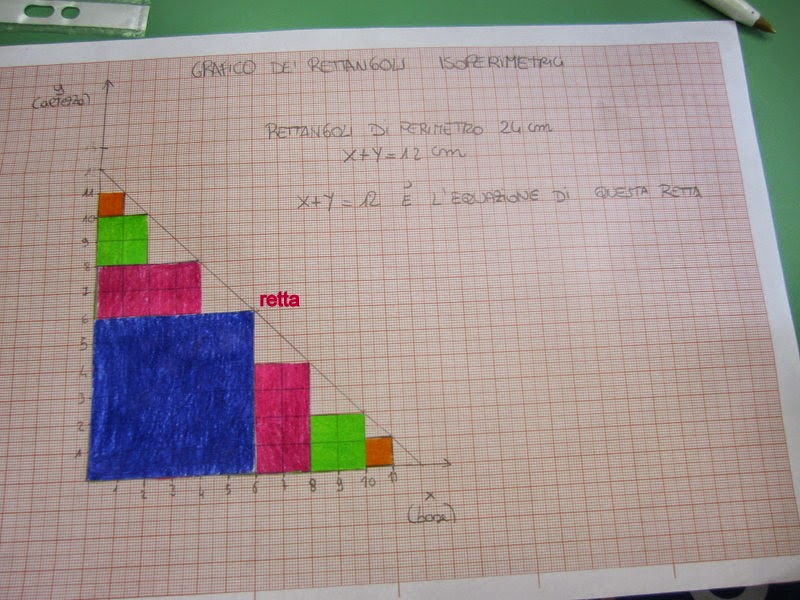
Dopo abbiamo disegnato, colorato e ritagliato rettangoli isoperimetrici di perimetro 24 cm. I rettangoli così ottenuti li abbiamo incollati su un piano cartesiano, facendo coincidere un vertice di ciascun poligono con l’origine degli assi.

Congiungendo i vertici liberi dei rettangoli incollati sul piano cartesiano abbiamo ottenuto una retta di equazione x + y = 12 dove x e y rappresentano la base e l’altezza dei rettangoli, pertanto x + y è pari al semiperimetro.

Allo stesso risultato si può arrivare usando il software di geometria dinamica Geogebra (1)

Trovata la risposta alla prima domanda, rimaneva ancora un'altra questione da verificare:

"Due o più rettangoli che hanno la stessa area hanno anche lo stesso perimetro?"

Abbiamo proseguito la nostra attività di gruppo questa volta disegnando, colorando e ritagliando rettangoli equivalenti di area 36 cm quadrati. I rettangoli ottenuti li abbiamo incollati su un piano cartesiano, facendo coincidere un vertice di ciascun poligono con l’origine degli assi.

Congiungendo i vertici liberi dei rettangoli incollati sul piano cartesiano questa volta abbiamo ottenuto una curva chiamata iperbole di equazione x*y = 36 dove x e y rappresentano la base e l’altezza dei rettangoli.

Anche questa volta possiamo giungere allo stesso risultato usando Geogebra (2)

Abbiamo quindi calcolato il perimetro dei rettangoli ottenuti trovando anche questa volta la risposta alla nostra domanda: 

"i perimetri di rettangoli equivalenti non sono tutti uguali"

Infine siamo arrivati alla conclusione che ... 

il rettangolo di perimetro minimo è il quadrato

La II^ A ... ovvero ...

Giordano, Madalina, Giulia, Ilaria, Alessio, Diego Junior, Andrea Valeria, Adria, Gianpaolo, Flavio, Federico, Aurora, Jari, Niccolò, Stefano, Beatrice, Lorenzo, Francesca, Antonietta, Julien, Emanuela, Serges, Cecilia, Francesco.